A laser beam expander is designed to increase the diameter of a collimated input beam to a larger collimated output beam. Beam expanders are used in applications such as laser scanning, interferometry, and remote sensing. Contemporary laser beam expander designs are afocal systems that developed from well-established optical telescope fundamentals. In such systems, the object rays, located at infinity, enter parallel to the optical axis of the internal optics and exit parallel to them as well. This means that there is no focal length to the entire system.
Theory: Laser Beam Expanders
In a laser beam expander design, the placement of the objective and image lenses is reversed. In the Keplerian beam expander design, the collimated input beam focuses to a spot between the objective and image lenses, producing a point within the system where the laser’s energy is concentrated (Figure 1). The focused spot heats the air between the lenses, deflecting light rays from their optical path, which can potentially lead to wavefront errors. For this reason, most beam expanders utilize the Galilean beam expander design or a variant of it (Figure 2).
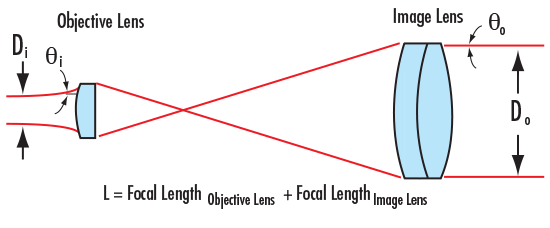
Figure 1: Keplerian Beam Expander
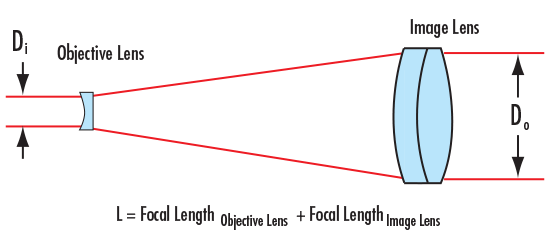
Figure 2: Galilean Beam Expander
When using the Keplerian or Galilean design in laser beam expander applications, it is important to be able to calculate the output beam divergence, which determines the deviation from a perfectly collimated source. The beam divergence is dependent upon the diameters of the input and output laser beams.

The Magnifying Power (MP) can now be expressed in terms of the Beam Divergences or Beam Diameters.
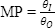
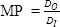
Interpreting the above equations, one sees that while the Output Beam Diameter (DO) increases, the Output Beam Divergence (θO) decreases and vice versa. Therefore, if you use the beam expander as a beam minimizer, the beam diameter will decrease but the divergence of the laser will increase. The price to pay for a small beam is a large divergence angle.
In addition to the above, it is important to be able to calculate the output beam diameter at a specific working distance (L). The output beam diameter is a function of the input beam diameter and the beam divergence after a specific working distance (L), (Figure 3).
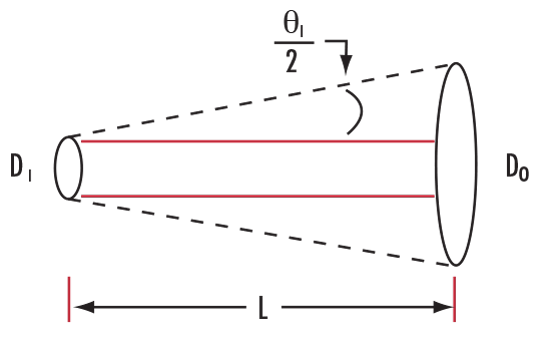
Figure 3: Calculating the Output Beam Diameter at a Specific Working Distance
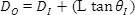
Laser beam divergence is specified in terms of a full angle, therefore, the above equation is expressed in terms of θI and not θI/2.
Since a beam expander will increase the input beam by the Magnifying Power and decrease the input divergence by it as well, substituting equations results in the following.
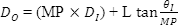
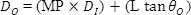
Application Example
Numerical example to explore previously mentioned beam expander equations.
Initial Parameters
Beam Expander Magnifying Power = MP = 10X
Input Beam Diameter = 1mm
Input Beam Divergence = 1mrad
Working Distance = L = 100m
Calculated Parameter
Output Beam Diameter
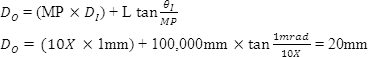
Compare this to the Beam Diameter without using a beam expander
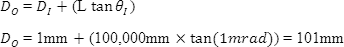
Although a beam expander will increase the input laser beam by a specific expansion power, it will also decrease the divergence by the same expansion power, resulting in a smaller collimated beam at a large distance.